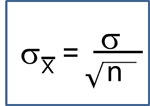Statistical Inference
We usually don't have information about all of the subjects in a population of interest, so we take samples from the population in order to make inferences about unknown population parameters .
.
An obvious concern would be how good a given sample's statistics are in estimating the characteristics of the population from which it was drawn. There are many factors that influence diastolic blood pressure levels, such as age, body weight, fitness, and heredity.
We would ideally like the sample to be representative of the population. Intuitively, it would seem preferable to have a random sample, meaning that all subjects in the population have an equal chance of being selected into the sample; this would minimize systematic errors caused by biased sampling.
In addition, it is also intuitive that small samples might not be representative of the population just by chance, and large samples are less likely to be affected by "the luck of the draw"; this would reduce so-called random error. Since we often rely on a single sample to estimate population parameters, we never actually know how good our estimates are. However, one can use sampling methods that reduce bias, and the degree of random error in a given sample can be estimated in order to get a sense of the precision of our estimates.