
Power and Sample Size Determination
Author:
Lisa Sullivan, PhD
Professor of Biosatistics
Boston Univeristy School of Public Health

A critically important aspect of any study is determining the appropriate sample size to answer the research question. This module will focus on formulas that can be used to estimate the sample size needed to produce a confidence interval estimate with a specified margin of error (precision) or to ensure that a test of hypothesis has a high probability of detecting a meaningful difference in the parameter.
Studies should be designed to include a sufficient number of participants to adequately address the research question. Studies that have either an inadequate number of participants or an excessively large number of participants are both wasteful in terms of participant and investigator time, resources to conduct the assessments, analytic efforts and so on. These situations can also be viewed as unethical as participants may have been put at risk as part of a study that was unable to answer an important question. Studies that are much larger than they need to be to answer the research questions are also wasteful.
The formulas presented here generate estimates of the necessary sample size(s) required based on statistical criteria. However, in many studies, the sample size is determined by financial or logistical constraints. For example, suppose a study is proposed to evaluate a new screening test for Down Syndrome. Suppose that the screening test is based on analysis of a blood sample taken from women early in pregnancy. In order to evaluate the properties of the screening test (e.g., the sensitivity and specificity), each pregnant woman will be asked to provide a blood sample and in addition to undergo an amniocentesis. The amniocentesis is included as the gold standard and the plan is to compare the results of the screening test to the results of the amniocentesis. Suppose that the collection and processing of the blood sample costs $250 per participant and that the amniocentesis costs $900 per participant. These financial constraints alone might substantially limit the number of women that can be enrolled. Just as it is important to consider both statistical and clinical significance when interpreting results of a statistical analysis, it is also important to weigh both statistical and logistical issues in determining the sample size for a study.
After completing this module, the student will be able to:

The module on confidence intervals provided methods for estimating confidence intervals for various parameters (e.g., μ , p, ( μ1 - μ2 ), μd , (p1-p2)). Confidence intervals for every parameter take the following general form:
Point Estimate + Margin of Error
In the module on confidence intervals we derived the formula for the confidence interval for μ as
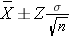
In practice we use the sample standard deviation to estimate the population standard deviation. Note that there is an alternative formula for estimating the mean of a continuous outcome in a single population, and it is used when the sample size is small (n<30). It involves a value from the t distribution, as opposed to one from the standard normal distribution, to reflect the desired level of confidence. When performing sample size computations, we use the large sample formula shown here. [Note: The resultant sample size might be small, and in the analysis stage, the appropriate confidence interval formula must be used.]
The point estimate for the population mean is the sample mean and the margin of error is
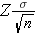
In planning studies, we want to determine the sample size needed to ensure that the margin of error is sufficiently small to be informative. For example, suppose we want to estimate the mean weight of female college students. We conduct a study and generate a 95% confidence interval as follows 125 + 40 pounds, or 85 to 165 pounds. The margin of error is so wide that the confidence interval is uninformative. To be informative, an investigator might want the margin of error to be no more than 5 or 10 pounds (meaning that the 95% confidence interval would have a width (lower limit to upper limit) of 10 or 20 pounds). In order to determine the sample size needed, the investigator must specify the desired margin of error. It is important to note that this is not a statistical issue, but a clinical or a practical one. For example, suppose we want to estimate the mean birth weight of infants born to mothers who smoke cigarettes during pregnancy. Birth weights in infants clearly have a much more restricted range than weights of female college students. Therefore, we would probably want to generate a confidence interval for the mean birth weight that has a margin of error not exceeding 1 or 2 pounds.
The margin of error in the one sample confidence interval for μ can be written as follows:
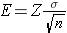 .
.
Our goal is to determine the sample size, n, that ensures that the margin of error, "E," does not exceed a specified value. We can take the formula above and, with some algebra, solve for n:
First, multipy both sides of the equation by the square root of n. Then cancel out the square root of n from the numerator and denominator on the right side of the equation (since any number divided by itself is equal to 1). This leaves:
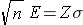
Now divide both sides by "E" and cancel out "E" from the numerator and denominator on the left side. This leaves:
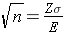
Finally, square both sides of the equation to get:
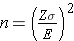
This formula generates the sample size, n, required to ensure that the margin of error, E, does not exceed a specified value. To solve for n, we must input "Z," "σ," and "E."
Sometimes it is difficult to estimate σ. When we use the sample size formula above (or one of the other formulas that we will present in the sections that follow), we are planning a study to estimate the unknown mean of a particular outcome variable in a population. It is unlikely that we would know the standard deviation of that variable. In sample size computations, investigators often use a value for the standard deviation from a previous study or a study done in a different, but comparable, population. The sample size computation is not an application of statistical inference and therefore it is reasonable to use an appropriate estimate for the standard deviation. The estimate can be derived from a different study that was reported in the literature; some investigators perform a small pilot study to estimate the standard deviation. A pilot study usually involves a small number of participants (e.g., n=10) who are selected by convenience, as opposed to by random sampling. Data from the participants in the pilot study can be used to compute a sample standard deviation, which serves as a good estimate for σ in the sample size formula. Regardless of how the estimate of the variability of the outcome is derived, it should always be conservative (i.e., as large as is reasonable), so that the resultant sample size is not too small.
The formula 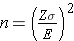 produces the minimum sample size to ensure that the margin of error in a confidence interval will not exceed E. In planning studies, investigators should also consider attrition or loss to follow-up. The formula above gives the number of participants needed with complete data to ensure that the margin of error in the confidence interval does not exceed E. We will illustrate how attrition is addressed in planning studies through examples in the following sections.
produces the minimum sample size to ensure that the margin of error in a confidence interval will not exceed E. In planning studies, investigators should also consider attrition or loss to follow-up. The formula above gives the number of participants needed with complete data to ensure that the margin of error in the confidence interval does not exceed E. We will illustrate how attrition is addressed in planning studies through examples in the following sections.
In studies where the plan is to estimate the mean of a continuous outcome variable in a single population, the formula for determining sample size is given below:
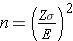
where Z is the value from the standard normal distribution reflecting the confidence level that will be used (e.g., Z = 1.96 for 95%), σ is the standard deviation of the outcome variable and E is the desired margin of error. The formula above generates the minimum number of subjects required to ensure that the margin of error in the confidence interval for μ does not exceed E.
Example 1:
An investigator wants to estimate the mean systolic blood pressure in children with congenital heart disease who are between the ages of 3 and 5. How many children should be enrolled in the study? The investigator plans on using a 95% confidence interval (so Z=1.96) and wants a margin of error of 5 units. The standard deviation of systolic blood pressure is unknown, but the investigators conduct a literature search and find that the standard deviation of systolic blood pressures in children with other cardiac defects is between 15 and 20. To estimate the sample size, we consider the larger standard deviation in order to obtain the most conservative (largest) sample size.
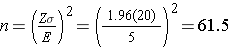
In order to ensure that the 95% confidence interval estimate of the mean systolic blood pressure in children between the ages of 3 and 5 with congenital heart disease is within 5 units of the true mean, a sample of size 62 is needed. [Note: We always round up; the sample size formulas always generate the minimum number of subjects needed to ensure the specified precision.] Had we assumed a standard deviation of 15, the sample size would have been n=35. Because the estimates of the standard deviation were derived from studies of children with other cardiac defects, it would be advisable to use the larger standard deviation and plan for a study with 62 children. Selecting the smaller sample size could potentially produce a confidence interval estimate with a larger margin of error.

An investigator wants to estimate the mean birth weight of infants born full term (approximately 40 weeks gestation) to mothers who are 19 years of age and under. The mean birth weight of infants born full-term to mothers 20 years of age and older is 3,510 grams with a standard deviation of 385 grams. How many women 19 years of age and under must be enrolled in the study to ensure that a 95% confidence interval estimate of the mean birth weight of their infants has a margin of error not exceeding 100 grams? Try to work through the calculation before you look at the answer.
Answer
In studies where the plan is to estimate the proportion of successes in a dichotomous outcome variable (yes/no) in a single population, the formula for determining sample size is:
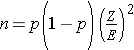
where Z is the value from the standard normal distribution reflecting the confidence level that will be used (e.g., Z = 1.96 for 95%) and E is the desired margin of error. p is the proportion of successes in the population. Here we are planning a study to generate a 95% confidence interval for the unknown population proportion, p. The equation to determine the sample size for determining p seems to require knowledge of p, but this is obviously this is a circular argument, because if we knew the proportion of successes in the population, then a study would not be necessary! What we really need is an approximate value of p or an anticipated value. The range of p is 0 to 1, and therefore the range of p(1-p) is 0 to 1. The value of p that maximizes p(1-p) is p=0.5. Consequently, if there is no information available to approximate p, then p=0.5 can be used to generate the most conservative, or largest, sample size.
Example 2:
An investigator wants to estimate the proportion of freshmen at his University who currently smoke cigarettes (i.e., the prevalence of smoking). How many freshmen should be involved in the study to ensure that a 95% confidence interval estimate of the proportion of freshmen who smoke is within 5% of the true proportion?
Because we have no information on the proportion of freshmen who smoke, we use 0.5 to estimate the sample size as follows:
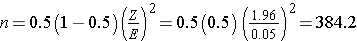
In order to ensure that the 95% confidence interval estimate of the proportion of freshmen who smoke is within 5% of the true proportion, a sample of size 385 is needed.

Suppose that a similar study was conducted 2 years ago and found that the prevalence of smoking was 27% among freshmen. If the investigator believes that this is a reasonable estimate of prevalence 2 years later, it can be used to plan the next study. Using this estimate of p, what sample size is needed (assuming that again a 95% confidence interval will be used and we want the same level of precision)?
Answer
Example 3:
An investigator wants to estimate the prevalence of breast cancer among women who are between 40 and 45 years of age living in Boston. How many women must be involved in the study to ensure that the estimate is precise? National data suggest that 1 in 235 women are diagnosed with breast cancer by age 40. This translates to a proportion of 0.0043 (0.43%) or a prevalence of 43 per 10,000 women. Suppose the investigator wants the estimate to be within 10 per 10,000 women with 95% confidence. The sample size is computed as follows:
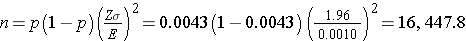
A sample of size n=16,448 will ensure that a 95% confidence interval estimate of the prevalence of breast cancer is within 0.10 (or to within 10 women per 10,000) of its true value. This is a situation where investigators might decide that a sample of this size is not feasible. Suppose that the investigators thought a sample of size 5,000 would be reasonable from a practical point of view. How precisely can we estimate the prevalence with a sample of size n=5,000? Recall that the confidence interval formula to estimate prevalence is:
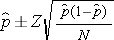 .
.
Assuming that the prevalence of breast cancer in the sample will be close to that based on national data, we would expect the margin of error to be approximately equal to the following:
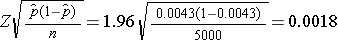
Thus, with n=5,000 women, a 95% confidence interval would be expected to have a margin of error of 0.0018 (or 18 per 10,000). The investigators must decide if this would be sufficiently precise to answer the research question. Note that the above is based on the assumption that the prevalence of breast cancer in Boston is similar to that reported nationally. This may or may not be a reasonable assumption. In fact, it is the objective of the current study to estimate the prevalence in Boston. The research team, with input from clinical investigators and biostatisticians, must carefully evaluate the implications of selecting a sample of size n = 5,000, n = 16,448 or any size in between.
In studies where the plan is to estimate the difference in means between two independent populations, the formula for determining the sample sizes required in each comparison group is given below:

where ni is the sample size required in each group (i=1,2), Z is the value from the standard normal distribution reflecting the confidence level that will be used and E is the desired margin of error. σ again reflects the standard deviation of the outcome variable. Recall from the module on confidence intervals that, when we generated a confidence interval estimate for the difference in means, we used Sp, the pooled estimate of the common standard deviation, as a measure of variability in the outcome (based on pooling the data), where Sp is computed as follows:
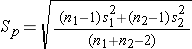
If data are available on variability of the outcome in each comparison group, then Sp can be computed and used in the sample size formula. However, it is more often the case that data on the variability of the outcome are available from only one group, often the untreated (e.g., placebo control) or unexposed group. When planning a clinical trial to investigate a new drug or procedure, data are often available from other trials that involved a placebo or an active control group (i.e., a standard medication or treatment given for the condition under study). The standard deviation of the outcome variable measured in patients assigned to the placebo, control or unexposed group can be used to plan a future trial, as illustrated below.
Note that the formula for the sample size generates sample size estimates for samples of equal size. If a study is planned where different numbers of patients will be assigned or different numbers of patients will comprise the comparison groups, then alternative formulas can be used.
Example 4:
An investigator wants to plan a clinical trial to evaluate the efficacy of a new drug designed to increase HDL cholesterol (the "good" cholesterol). The plan is to enroll participants and to randomly assign them to receive either the new drug or a placebo. HDL cholesterol will be measured in each participant after 12 weeks on the assigned treatment. Based on prior experience with similar trials, the investigator expects that 10% of all participants will be lost to follow up or will drop out of the study over 12 weeks. A 95% confidence interval will be estimated to quantify the difference in mean HDL levels between patients taking the new drug as compared to placebo. The investigator would like the margin of error to be no more than 3 units. How many patients should be recruited into the study?
The sample sizes are computed as follows:

A major issue is determining the variability in the outcome of interest (σ), here the standard deviation of HDL cholesterol. To plan this study, we can use data from the Framingham Heart Study. In participants who attended the seventh examination of the Offspring Study and were not on treatment for high cholesterol, the standard deviation of HDL cholesterol is 17.1. We will use this value and the other inputs to compute the sample sizes as follows:
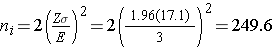
Samples of size n1=250 and n2=250 will ensure that the 95% confidence interval for the difference in mean HDL levels will have a margin of error of no more than 3 units. Again, these sample sizes refer to the numbers of participants with complete data. The investigators hypothesized a 10% attrition (or drop-out) rate (in both groups). In order to ensure that the total sample size of 500 is available at 12 weeks, the investigator needs to recruit more participants to allow for attrition.
N (number to enroll) * (% retained) = desired sample size
Therefore N (number to enroll) = desired sample size/(% retained)
N = 500/0.90 = 556
If they anticipate a 10% attrition rate, the investigators should enroll 556 participants. This will ensure N=500 with complete data at the end of the trial.
Example 5:
An investigator wants to compare two diet programs in children who are obese. One diet is a low fat diet, and the other is a low carbohydrate diet. The plan is to enroll children and weigh them at the start of the study. Each child will then be randomly assigned to either the low fat or the low carbohydrate diet. Each child will follow the assigned diet for 8 weeks, at which time they will again be weighed. The number of pounds lost will be computed for each child. Based on data reported from diet trials in adults, the investigator expects that 20% of all children will not complete the study. A 95% confidence interval will be estimated to quantify the difference in weight lost between the two diets and the investigator would like the margin of error to be no more than 3 pounds. How many children should be recruited into the study?
The sample sizes are computed as follows:

Again the issue is determining the variability in the outcome of interest (σ), here the standard deviation in pounds lost over 8 weeks. To plan this study, investigators use data from a published study in adults. Suppose one such study compared the same diets in adults and involved 100 participants in each diet group. The study reported a standard deviation in weight lost over 8 weeks on a low fat diet of 8.4 pounds and a standard deviation in weight lost over 8 weeks on a low carbohydrate diet of 7.7 pounds. These data can be used to estimate the common standard deviation in weight lost as follows:
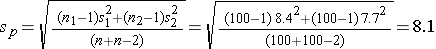
We now use this value and the other inputs to compute the sample sizes:
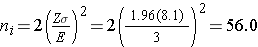
Samples of size n1=56 and n2=56 will ensure that the 95% confidence interval for the difference in weight lost between diets will have a margin of error of no more than 3 pounds. Again, these sample sizes refer to the numbers of children with complete data. The investigators anticipate a 20% attrition rate. In order to ensure that the total sample size of 112 is available at 8 weeks, the investigator needs to recruit more participants to allow for attrition.
N (number to enroll) * (% retained) = desired sample size
Therefore N (number to enroll) = desired sample size/(% retained)
N = 112/0.80 = 140
In studies where the plan is to estimate the mean difference of a continuous outcome based on matched data, the formula for determining sample size is given below:
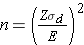
where Z is the value from the standard normal distribution reflecting the confidence level that will be used (e.g., Z = 1.96 for 95%), E is the desired margin of error, and σd is the standard deviation of the difference scores. It is extremely important that the standard deviation of the difference scores (e.g., the difference based on measurements over time or the difference between matched pairs) is used here to appropriately estimate the sample size.
In studies where the plan is to estimate the difference in proportions between two independent populations (i.e., to estimate the risk difference), the formula for determining the sample sizes required in each comparison group is:
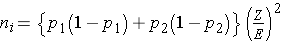
where ni is the sample size required in each group (i=1,2), Z is the value from the standard normal distribution reflecting the confidence level that will be used (e.g., Z = 1.96 for 95%), and E is the desired margin of error. p1 and p2 are the proportions of successes in each comparison group. Again, here we are planning a study to generate a 95% confidence interval for the difference in unknown proportions, and the formula to estimate the sample sizes needed requires p1 and p2. In order to estimate the sample size, we need approximate values of p1 and p2. The values of p1 and p2 that maximize the sample size are p1=p2=0.5. Thus, if there is no information available to approximate p1 and p2, then 0.5 can be used to generate the most conservative, or largest, sample sizes.
Similar to the situation for two independent samples and a continuous outcome at the top of this page, it may be the case that data are available on the proportion of successes in one group, usually the untreated (e.g., placebo control) or unexposed group. If so, the known proportion can be used for both p1 and p2 in the formula shown above. The formula shown above generates sample size estimates for samples of equal size. If a study is planned where different numbers of patients will be assigned or different numbers of patients will comprise the comparison groups, then alternative formulas can be used. Interested readers can see Fleiss for more details.4
Example 6:
An investigator wants to estimate the impact of smoking during pregnancy on premature delivery. Normal pregnancies last approximately 40 weeks and premature deliveries are those that occur before 37 weeks. The 2005 National Vital Statistics report indicates that approximately 12% of infants are born prematurely in the United States.5 The investigator plans to collect data through medical record review and to generate a 95% confidence interval for the difference in proportions of infants born prematurely to women who smoked during pregnancy as compared to those who did not. How many women should be enrolled in the study to ensure that the 95% confidence interval for the difference in proportions has a margin of error of no more than 4%?
The sample sizes (i.e., numbers of women who smoked and did not smoke during pregnancy) can be computed using the formula shown above. National data suggest that 12% of infants are born prematurely. We will use that estimate for both groups in the sample size computation.
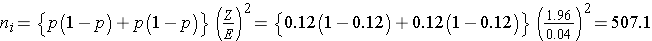
Samples of size n1=508 women who smoked during pregnancy and n2=508 women who did not smoke during pregnancy will ensure that the 95% confidence interval for the difference in proportions who deliver prematurely will have a margin of error of no more than 4%.

Is attrition an issue here?
Answer
In the module on hypothesis testing for means and proportions, we introduced techniques for means, proportions, differences in means, and differences in proportions. While each test involved details that were specific to the outcome of interest (e.g., continuous or dichotomous) and to the number of comparison groups (one, two, more than two), there were common elements to each test. For example, in each test of hypothesis, there are two errors that can be committed. The first is called a Type I error and refers to the situation where we incorrectly reject H0 when in fact it is true. In the first step of any test of hypothesis, we select a level of significance, α , and α = P(Type I error) = P(Reject H0 | H0 is true). Because we purposely select a small value for α , we control the probability of committing a Type I error. The second type of error is called a Type II error and it is defined as the probability we do not reject H0 when it is false. The probability of a Type II error is denoted β , and β =P(Type II error) = P(Do not Reject H0 | H0 is false). In hypothesis testing, we usually focus on power, which is defined as the probability that we reject H0 when it is false, i.e., power = 1- β = P(Reject H0 | H0 is false). Power is the probability that a test correctly rejects a false null hypothesis. A good test is one with low probability of committing a Type I error (i.e., small α ) and high power (i.e., small β, high power).
Here we present formulas to determine the sample size required to ensure that a test has high power. The sample size computations depend on the level of significance, aα, the desired power of the test (equivalent to 1-β), the variability of the outcome, and the effect size. The effect size is the difference in the parameter of interest that represents a clinically meaningful difference. Similar to the margin of error in confidence interval applications, the effect size is determined based on clinical or practical criteria and not statistical criteria.
The concept of statistical power can be difficult to grasp. Before presenting the formulas to determine the sample sizes required to ensure high power in a test, we will first discuss power from a conceptual point of view.
Suppose we want to test the following hypotheses at aα=0.05: H0: μ = 90 versus H1: μ ≠ 90. To test the hypotheses, suppose we select a sample of size n=100. For this example, assume that the standard deviation of the outcome is σ=20. We compute the sample mean and then must decide whether the sample mean provides evidence to support the alternative hypothesis or not. This is done by computing a test statistic and comparing the test statistic to an appropriate critical value. If the null hypothesis is true (μ=90), then we are likely to select a sample whose mean is close in value to 90. However, it is also possible to select a sample whose mean is much larger or much smaller than 90. Recall from the Central Limit Theorem (see page 11 in the module on Probability), that for large n (here n=100 is sufficiently large), the distribution of the sample means is approximately normal with a mean of
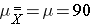
and
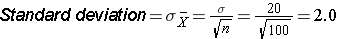
If the null hypothesis is true, it is possible to observe any sample mean shown in the figure below; all are possible under H0: μ = 90.
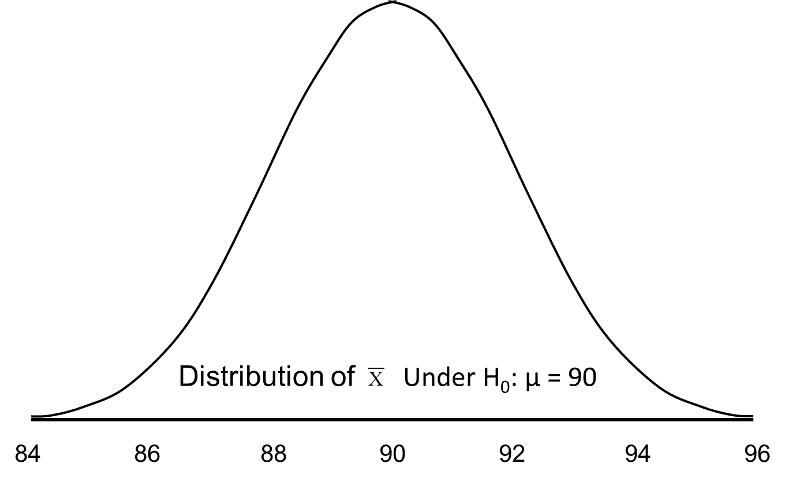
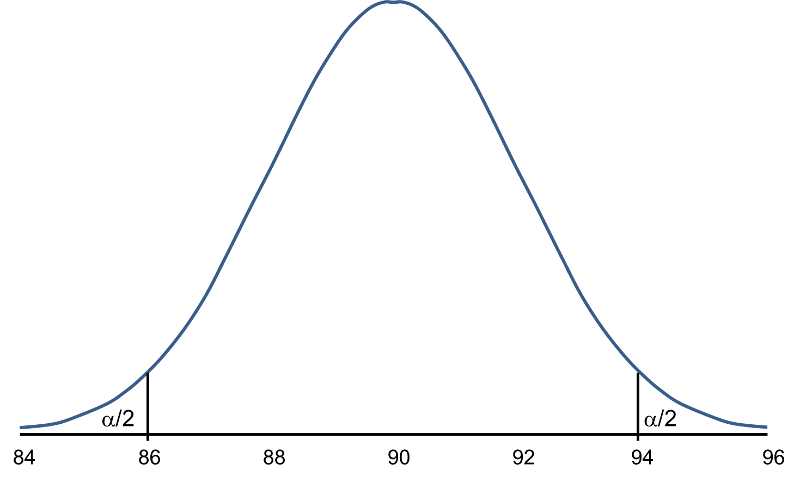
When we set up the decision rule for our test of hypothesis, we determine critical values based on α=0.05 and a two-sided test. When we run tests of hypotheses, we usually standardize the data (e.g., convert to Z or t) and the critical values are appropriate values from the probability distribution used in the test. To facilitate interpretation, we will continue this discussion with ![]() as opposed to Z. The critical values for a two-sided test with α=0.05 are 86.06 and 93.92 (these values correspond to -1.96 and 1.96, respectively, on the Z scale), so the decision rule is as follows: Reject H0 if
as opposed to Z. The critical values for a two-sided test with α=0.05 are 86.06 and 93.92 (these values correspond to -1.96 and 1.96, respectively, on the Z scale), so the decision rule is as follows: Reject H0 if ![]() < 86.06 or if
< 86.06 or if ![]() > 93.92. The rejection region is shown in the tails of the figure below.
> 93.92. The rejection region is shown in the tails of the figure below.
Rejection Region for Test H0: μ = 90 versus H1: μ ≠ 90 at α =0.05
 .
.
The areas in the two tails of the curve represent the probability of a Type I Error, α= 0.05. This concept was discussed in the module on Hypothesis Testing.
Now, suppose that the alternative hypothesis, H1, is true (i.e., μ ≠ 90) and that the true mean is actually 94. The figure below shows the distributions of the sample mean under the null and alternative hypotheses.The values of the sample mean are shown along the horizontal axis.
Distribution of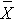 Under H0: μ = 90 and Under H1: μ = 94
Under H0: μ = 90 and Under H1: μ = 94
If the true mean is 94, then the alternative hypothesis is true. In our test, we selected α = 0.05 and reject H0 if the observed sample mean exceeds 93.92 (focusing on the upper tail of the rejection region for now). The critical value (93.92) is indicated by the vertical line. The probability of a Type II error is denoted β, and β = P(Do not Reject H0 | H0 is false), i.e., the probability of not rejecting the null hypothesis if the null hypothesis were true. β is shown in the figure above as the area under the rightmost curve (H1) to the left of the vertical line (where we do not reject H0). Power is defined as 1- β = P(Reject H0 | H0 is false) and is shown in the figure as the area under the rightmost curve (H1) to the right of the vertical line (where we reject H0 ).
Note that β and power are related to α, the variability of the outcome and the effect size. From the figure above we can see what happens to β and power if we increase α. Suppose, for example, we increase α to α=0.10.The upper critical value would be 92.56 instead of 93.92. The vertical line would shift to the left, increasing α, decreasing β and increasing power. While a better test is one with higher power, it is not advisable to increase α as a means to increase power. Nonetheless, there is a direct relationship between α and power (as α increases, so does power).
β and power are also related to the variability of the outcome and to the effect size. The effect size is the difference in the parameter of interest (e.g., μ) that represents a clinically meaningful difference. The figure above graphically displays α, β, and power when the difference in the mean under the null as compared to the alternative hypothesis is 4 units (i.e., 90 versus 94). The figure below shows the same components for the situation where the mean under the alternative hypothesis is 98.
Figure - Distribution of Under H0: μ = 90 and Under H1: μ = 98.
Under H0: μ = 90 and Under H1: μ = 98.
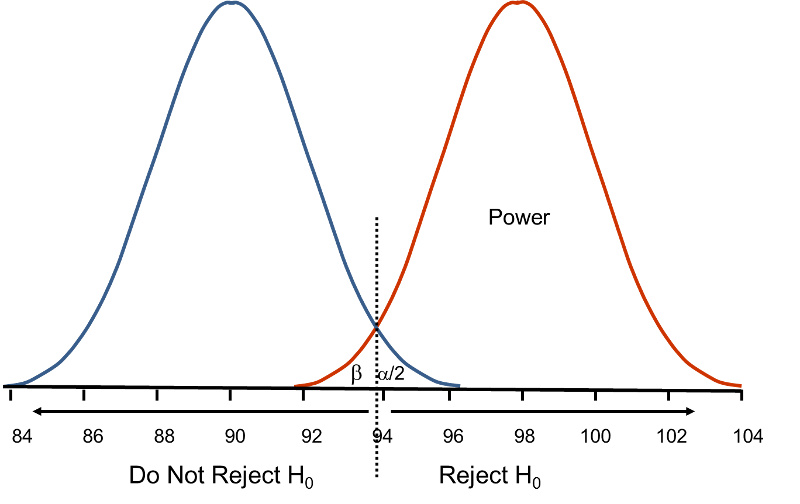
Notice that there is much higher power when there is a larger difference between the mean under H0 as compared to H1 (i.e., 90 versus 98). A statistical test is much more likely to reject the null hypothesis in favor of the alternative if the true mean is 98 than if the true mean is 94. Notice also in this case that there is little overlap in the distributions under the null and alternative hypotheses. If a sample mean of 97 or higher is observed it is very unlikely that it came from a distribution whose mean is 90. In the previous figure for H0: μ = 90 and H1: μ = 94, if we observed a sample mean of 93, for example, it would not be as clear as to whether it came from a distribution whose mean is 90 or one whose mean is 94.
In designing studies most people consider power of 80% or 90% (just as we generally use 95% as the confidence level for confidence interval estimates). The inputs for the sample size formulas include the desired power, the level of significance and the effect size. The effect size is selected to represent a clinically meaningful or practically important difference in the parameter of interest, as we will illustrate.
The formulas we present below produce the minimum sample size to ensure that the test of hypothesis will have a specified probability of rejecting the null hypothesis when it is false (i.e., a specified power). In planning studies, investigators again must account for attrition or loss to follow-up. The formulas shown below produce the number of participants needed with complete data, and we will illustrate how attrition is addressed in planning studies.
In studies where the plan is to perform a test of hypothesis comparing the mean of a continuous outcome variable in a single population to a known mean, the hypotheses of interest are:
H0: μ = μ 0 and H1: μ ≠ μ 0 where μ 0 is the known mean (e.g., a historical control). The formula for determining sample size to ensure that the test has a specified power is given below:
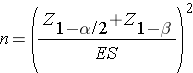
where α is the selected level of significance and Z 1-α /2 is the value from the standard normal distribution holding 1- α/2 below it. For example, if α=0.05, then 1- α/2 = 0.975 and Z=1.960. 1- β is the selected power, and Z 1-β is the value from the standard normal distribution holding 1- β below it. Sample size estimates for hypothesis testing are often based on achieving 80% or 90% power. The Z 1-β values for these popular scenarios are given below:
ES is the effect size, defined as follows:
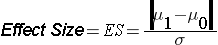
where μ 0 is the mean under H0, μ 1 is the mean under H1 and σ is the standard deviation of the outcome of interest. The numerator of the effect size, the absolute value of the difference in means | μ 1 - μ 0 |, represents what is considered a clinically meaningful or practically important difference in means. Similar to the issue we faced when planning studies to estimate confidence intervals, it can sometimes be difficult to estimate the standard deviation. In sample size computations, investigators often use a value for the standard deviation from a previous study or a study performed in a different but comparable population. Regardless of how the estimate of the variability of the outcome is derived, it should always be conservative (i.e., as large as is reasonable), so that the resultant sample size will not be too small.
Example 7:
An investigator hypothesizes that in people free of diabetes, fasting blood glucose, a risk factor for coronary heart disease, is higher in those who drink at least 2 cups of coffee per day. A cross-sectional study is planned to assess the mean fasting blood glucose levels in people who drink at least two cups of coffee per day. The mean fasting blood glucose level in people free of diabetes is reported as 95.0 mg/dL with a standard deviation of 9.8 mg/dL.7 If the mean blood glucose level in people who drink at least 2 cups of coffee per day is 100 mg/dL, this would be important clinically. How many patients should be enrolled in the study to ensure that the power of the test is 80% to detect this difference? A two sided test will be used with a 5% level of significance.
The effect size is computed as:
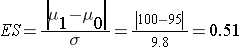 .
.
The effect size represents the meaningful difference in the population mean - here 95 versus 100, or 0.51 standard deviation units different. We now substitute the effect size and the appropriate Z values for the selected α and power to compute the sample size.
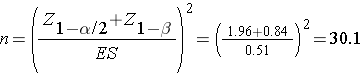
Therefore, a sample of size n=31 will ensure that a two-sided test with α =0.05 has 80% power to detect a 5 mg/dL difference in mean fasting blood glucose levels.
In the planned study, participants will be asked to fast overnight and to provide a blood sample for analysis of glucose levels. Based on prior experience, the investigators hypothesize that 10% of the participants will fail to fast or will refuse to follow the study protocol. Therefore, a total of 35 participants will be enrolled in the study to ensure that 31 are available for analysis (see below).
N (number to enroll) * (% following protocol) = desired sample size
Therefore N (number to enroll) = desired sample size/(% retained)
N = 31/0.90 = 35.
In studies where the plan is to perform a test of hypothesis comparing the proportion of successes in a dichotomous outcome variable in a single population to a known proportion, the hypotheses of interest are:
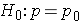
versus
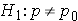
where p0 is the known proportion (e.g., a historical control). The formula for determining the sample size to ensure that the test has a specified power is given below:
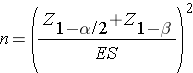
where α is the selected level of significance and Z 1-α /2 is the value from the standard normal distribution holding 1- α/2 below it. 1- β is the selected power and Z 1-β is the value from the standard normal distribution holding 1- β below it , and ES is the effect size, defined as follows:
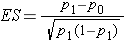
where p0 is the proportion under H0 and p1 is the proportion under H1. The numerator of the effect size, the absolute value of the difference in proportions |p1-p0|, again represents what is considered a clinically meaningful or practically important difference in proportions.
Example 8:
A recent report from the Framingham Heart Study indicated that 26% of people free of cardiovascular disease had elevated LDL cholesterol levels, defined as LDL > 159 mg/dL.9 An investigator hypothesizes that a higher proportion of patients with a history of cardiovascular disease will have elevated LDL cholesterol. How many patients should be studied to ensure that the power of the test is 90% to detect a 5% difference in the proportion with elevated LDL cholesterol? A two sided test will be used with a 5% level of significance.
We first compute the effect size:
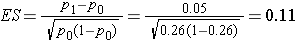
We now substitute the effect size and the appropriate Z values for the selected α and power to compute the sample size.
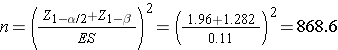
A sample of size n=869 will ensure that a two-sided test with α =0.05 has 90% power to detect a 5% difference in the proportion of patients with a history of cardiovascular disease who have an elevated LDL cholesterol level.

A medical device manufacturer produces implantable stents. During the manufacturing process, approximately 10% of the stents are deemed to be defective. The manufacturer wants to test whether the proportion of defective stents is more than 10%. If the process produces more than 15% defective stents, then corrective action must be taken. Therefore, the manufacturer wants the test to have 90% power to detect a difference in proportions of this magnitude. How many stents must be evaluated? For you computations, use a two-sided test with a 5% level of significance. (Do the computation yourself, before looking at the answer.)
Answer
In studies where the plan is to perform a test of hypothesis comparing the means of a continuous outcome variable in two independent populations, the hypotheses of interest are:
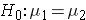
versus
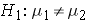
where μ 1 and μ 2 are the means in the two comparison populations. The formula for determining the sample sizes to ensure that the test has a specified power is:
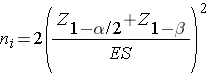
where ni is the sample size required in each group (i=1,2), α is the selected level of significance and Z 1-α /2 is the value from the standard normal distribution holding 1- α /2 below it, and 1- β is the selected power and Z 1-β is the value from the standard normal distribution holding 1- β below it. ES is the effect size, defined as:
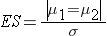
where | μ 1 - μ 2 | is the absolute value of the difference in means between the two groups expected under the alternative hypothesis, H1. σ is the standard deviation of the outcome of interest. Recall from the module on Hypothesis Testing that, when we performed tests of hypothesis comparing the means of two independent groups, we used Sp, the pooled estimate of the common standard deviation, as a measure of variability in the outcome.
Sp is computed as follows:
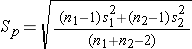
If data are available on variability of the outcome in each comparison group, then Sp can be computed and used to generate the sample sizes. However, it is more often the case that data on the variability of the outcome are available from only one group, usually the untreated (e.g., placebo control) or unexposed group. When planning a clinical trial to investigate a new drug or procedure, data are often available from other trials that may have involved a placebo or an active control group (i.e., a standard medication or treatment given for the condition under study). The standard deviation of the outcome variable measured in patients assigned to the placebo, control or unexposed group can be used to plan a future trial, as illustrated.
Note also that the formula shown above generates sample size estimates for samples of equal size. If a study is planned where different numbers of patients will be assigned or different numbers of patients will comprise the comparison groups, then alternative formulas can be used (see Howell3 for more details).
Example 9:
An investigator is planning a clinical trial to evaluate the efficacy of a new drug designed to reduce systolic blood pressure. The plan is to enroll participants and to randomly assign them to receive either the new drug or a placebo. Systolic blood pressures will be measured in each participant after 12 weeks on the assigned treatment. Based on prior experience with similar trials, the investigator expects that 10% of all participants will be lost to follow up or will drop out of the study. If the new drug shows a 5 unit reduction in mean systolic blood pressure, this would represent a clinically meaningful reduction. How many patients should be enrolled in the trial to ensure that the power of the test is 80% to detect this difference? A two sided test will be used with a 5% level of significance.
In order to compute the effect size, an estimate of the variability in systolic blood pressures is needed. Analysis of data from the Framingham Heart Study showed that the standard deviation of systolic blood pressure was 19.0. This value can be used to plan the trial.
The effect size is:
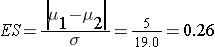
We now substitute the effect size and the appropriate Z values for the selected α and power to compute the sample size.
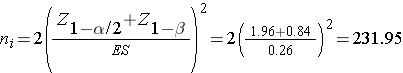
Samples of size n1=232 and n2= 232 will ensure that the test of hypothesis will have 80% power to detect a 5 unit difference in mean systolic blood pressures in patients receiving the new drug as compared to patients receiving the placebo. However, the investigators hypothesized a 10% attrition rate (in both groups), and to ensure a total sample size of 232 they need to allow for attrition.
N (number to enroll) * (% retained) = desired sample size
Therefore N (number to enroll) = desired sample size/(% retained)
N = 232/0.90 = 258.
The investigator must enroll 258 participants to be randomly assigned to receive either the new drug or placebo.

An investigator is planning a study to assess the association between alcohol consumption and grade point average among college seniors. The plan is to categorize students as heavy drinkers or not using 5 or more drinks on a typical drinking day as the criterion for heavy drinking. Mean grade point averages will be compared between students classified as heavy drinkers versus not using a two independent samples test of means. The standard deviation in grade point averages is assumed to be 0.42 and a meaningful difference in grade point averages (relative to drinking status) is 0.25 units. How many college seniors should be enrolled in the study to ensure that the power of the test is 80% to detect a 0.25 unit difference in mean grade point averages? Use a two-sided test with a 5% level of significance.
Answer
In studies where the plan is to perform a test of hypothesis on the mean difference in a continuous outcome variable based on matched data, the hypotheses of interest are:
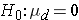
versus
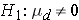
where μd is the mean difference in the population. The formula for determining the sample size to ensure that the test has a specified power is given below:
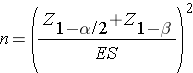
where α is the selected level of significance and Z1-α/2 is the value from the standard normal distribution holding 1- α/2 below it, 1- β is the selected power and Z1-β is the value from the standard normal distribution holding 1- β below it and ES is the effect size, defined as follows:
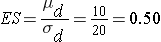
where μd is the mean difference expected under the alternative hypothesis, H1, and σd is the standard deviation of the difference in the outcome (e.g., the difference based on measurements over time or the difference between matched pairs).
Example 10:
An investigator wants to evaluate the efficacy of an acupuncture treatment for reducing pain in patients with chronic migraine headaches. The plan is to enroll patients who suffer from migraine headaches. Each will be asked to rate the severity of the pain they experience with their next migraine before any treatment is administered. Pain will be recorded on a scale of 1-100 with higher scores indicative of more severe pain. Each patient will then undergo the acupuncture treatment. On their next migraine (post-treatment), each patient will again be asked to rate the severity of the pain. The difference in pain will be computed for each patient. A two sided test of hypothesis will be conducted, at α =0.05, to assess whether there is a statistically significant difference in pain scores before and after treatment. How many patients should be involved in the study to ensure that the test has 80% power to detect a difference of 10 units on the pain scale? Assume that the standard deviation in the difference scores is approximately 20 units.
First compute the effect size:
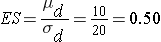
Then substitute the effect size and the appropriate Z values for the selected α and power to compute the sample size.
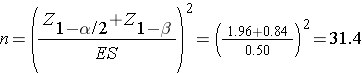
A sample of size n=32 patients with migraine will ensure that a two-sided test with α =0.05 has 80% power to detect a mean difference of 10 points in pain before and after treatment, assuming that all 32 patients complete the treatment.
In studies where the plan is to perform a test of hypothesis comparing the proportions of successes in two independent populations, the hypotheses of interest are:
H0: p1 = p2 versus H1: p1 ≠ p2
where p 1 and p2 are the proportions in the two comparison populations. The formula for determining the sample sizes to ensure that the test has a specified power is given below:
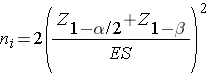
where ni is the sample size required in each group (i=1,2), α is the selected level of significance and Z1-α/2 is the value from the standard normal distribution holding 1- α/2 below it, and 1- β is the selected power and Z1-β is the value from the standard normal distribution holding 1- β below it. ES is the effect size, defined as follows:
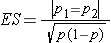 ,
,
where |p1 - p2| is the absolute value of the difference in proportions between the two groups expected under the alternative hypothesis, H1, and p is the overall proportion, based on pooling the data from the two comparison groups (p can be computed by taking the mean of the proportions in the two comparison groups, assuming that the groups will be of approximately equal size).
Example 11:
An investigator hypothesizes that there is a higher incidence of flu among students who use their athletic facility regularly than their counterparts who do not. The study will be conducted in the spring. Each student will be asked if they used the athletic facility regularly over the past 6 months and whether or not they had the flu. A test of hypothesis will be conducted to compare the proportion of students who used the athletic facility regularly and got flu with the proportion of students who did not and got flu. During a typical year, approximately 35% of the students experience flu. The investigators feel that a 30% increase in flu among those who used the athletic facility regularly would be clinically meaningful. How many students should be enrolled in the study to ensure that the power of the test is 80% to detect this difference in the proportions? A two sided test will be used with a 5% level of significance.
We first compute the effect size by substituting the proportions of students in each group who are expected to develop flu, p1=0.46 (i.e., 0.35*1.30=0.46) and p2=0.35 and the overall proportion, p=0.41 (i.e., (0.46+0.35)/2):
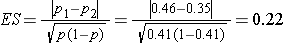
We now substitute the effect size and the appropriate Z values for the selected α and power to compute the sample size.
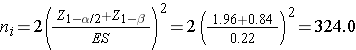
Samples of size n1=324 and n2=324 will ensure that the test of hypothesis will have 80% power to detect a 30% difference in the proportions of students who develop flu between those who do and do not use the athletic facilities regularly.

Donor Feces? Really? Clostridium difficile (also referred to as "C. difficile" or "C. diff.") is a bacterial species that can be found in the colon of humans, although its numbers are kept in check by other normal flora in the colon. Antibiotic therapy sometimes diminishes the normal flora in the colon to the point that C. difficile flourishes and causes infection with symptoms ranging from diarrhea to life-threatening inflammation of the colon. Illness from C. difficile most commonly affects older adults in hospitals or in long term care facilities and typically occurs after use of antibiotic medications. In recent years, C. difficile infections have become more frequent, more severe and more difficult to treat. Ironically, C. difficile is first treated by discontinuing antibiotics, if they are still being prescribed. If that is unsuccessful, the infection has been treated by switching to another antibiotic. However, treatment with another antibiotic frequently does not cure the C. difficile infection. There have been sporadic reports of successful treatment by infusing feces from healthy donors into the duodenum of patients suffering from C. difficile. (Yuk!) This re-establishes the normal microbiota in the colon, and counteracts the overgrowth of C. diff. The efficacy of this approach was tested in a randomized clinical trial reported in the New England Journal of Medicine (Jan. 2013). The investigators planned to randomly assign patients with recurrent C. difficile infection to either antibiotic therapy or to duodenal infusion of donor feces. In order to estimate the sample size that would be needed, the investigators assumed that the feces infusion would be successful 90% of the time, and antibiotic therapy would be successful in 60% of cases. How many subjects will be needed in each group to ensure that the power of the study is 80% with a level of significance α = 0.05?
Answer
Determining the appropriate design of a study is more important than the statistical analysis; a poorly designed study can never be salvaged, whereas a poorly analyzed study can be re-analyzed. A critical component in study design is the determination of the appropriate sample size. The sample size must be large enough to adequately answer the research question, yet not too large so as to involve too many patients when fewer would have sufficed. The determination of the appropriate sample size involves statistical criteria as well as clinical or practical considerations. Sample size determination involves teamwork; biostatisticians must work closely with clinical investigators to determine the sample size that will address the research question of interest with adequate precision or power to produce results that are clinically meaningful.
The following table summarizes the sample size formulas for each scenario described here. The formulas are organized by the proposed analysis, a confidence interval estimate or a test of hypothesis.
|
Situation |
Sample Size to Estimate Confidence Interval |
Sample Size to Conduct Test of Hypothesis |
|---|---|---|
|
Continuous Outcome, One Sample: CI for μ, H0: μ = μ0 |
|
|
|
Continuous Outcome, Two Independent Samples: CI for ( μ1-μ2), H0: μ1 = μ2 |
|
|
|
Continuous Outcome, Two Matched Samples: CI for μd , H0: μd = 0 |
|
|
|
Dichotomous Outcome, One Sample: CI for p , H0: p = p0 |
|
|
|
Dichotomous Outcome, Two Independent Samples: CI for (p1-p2) , H0: p1 = p2 |
|
|
An investigator wants to estimate the mean birth weight of infants born full term (approximately 40 weeks gestation) to mothers who are 19 years of age and under. The mean birth weight of infants born full-term to mothers 20 years of age and older is 3,510 grams with a standard deviation of 385 grams. How many women 19 years of age and under must be enrolled in the study to ensure that a 95% confidence interval estimate of the mean birth weight of their infants has a margin of error not exceeding 100 grams?
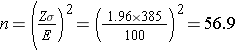
In order to ensure that the 95% confidence interval estimate of the mean birthweight is within 100 grams of the true mean, a sample of size 57 is needed. In planning the study, the investigator must consider the fact that some women may deliver prematurely. If women are enrolled into the study during pregnancy, then more than 57 women will need to be enrolled so that after excluding those who deliver prematurely, 57 with outcome information will be available for analysis. For example, if 5% of the women are expected to delivery prematurely (i.e., 95% will deliver full term), then 60 women must be enrolled to ensure that 57 deliver full term. The number of women that must be enrolled, N, is computed as follows:
N (number to enroll) * (% retained) = desired sample size
N (0.95) = 57
N = 57/0.95 = 60.
Suppose that a similar study was conducted 2 years ago and found that the prevalence of smoking was 27% among freshmen. If the investigator believes that this is a reasonable estimate of prevalence 2 years later, it can be used to plan the next study. Using this estimate of p, what sample size is needed (assuming that again a 95% confidence interval will be used and we want the same level of precision)?
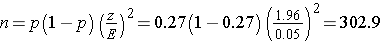
In order to ensure that the 95% confidence interval estimate of the proportion of freshmen who smoke is within 5% of the true proportion, a sample of size 303 is needed. Notice that this sample size is substantially smaller than the one estimated above. Having some information on the magnitude of the proportion in the population will always produce a sample size that is less than or equal to the one based on a population proportion of 0.5. However, the estimate must be realistic.
A medical device manufacturer produces implantable stents. During the manufacturing process, approximately 10% of the stents are deemed to be defective. The manufacturer wants to test whether the proportion of defective stents is more than 10%. If the process produces more than 15% defective stents, then corrective action must be taken. Therefore, the manufacturer wants the test to have 90% power to detect a difference in proportions of this magnitude. How many stents must be evaluated? For you computations, use a two-sided test with a 5% level of significance.
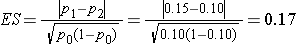
Then substitute the effect size and the appropriate z values for the selected alpha and power to comute the sample size.
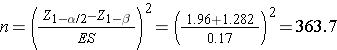
A sample size of 364 stents will ensure that a two-sided test with α=0.05 has 90% power to detect a 0.05, or 5%, difference in jthe proportion of defective stents produced.
An investigator is planning a study to assess the association between alcohol consumption and grade point average among college seniors. The plan is to categorize students as heavy drinkers or not using 5 or more drinks on a typical drinking day as the criterion for heavy drinking. Mean grade point averages will be compared between students classified as heavy drinkers versus not using a two independent samples test of means. The standard deviation in grade point averages is assumed to be 0.42 and a meaningful difference in grade point averages (relative to drinking status) is 0.25 units. How many college seniors should be enrolled in the study to ensure that the power of the test is 80% to detect a 0.25 unit difference in mean grade point averages? Use a two-sided test with a 5% level of significance.
First compute the effect size.
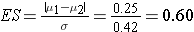
Now substitute the effect size and the appropriate z values for alpha and power to compute the sample size.
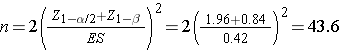
Sample sizes of ni=44 heavy drinkers and 44 who drink few fewer than five drinks per typical drinking day will ensure that the test of hypothesis has 80% power to detect a 0.25 unit difference in mean grade point averages.
We first compute the effect size by substituting the proportions of patients expected to be cured with each treatment, p1=0.6 and p2=0.9, and the overall proportion, p=0.75:
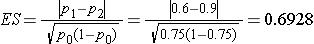
We now substitute the effect size and the appropriate Z values for the selected a and power to compute the sample size.
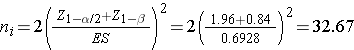
Samples of size n1=33 and n2=33 will ensure that the test of hypothesis will have 80% power to detect this difference in the proportions of patients who are cured of C. diff. by feces infusion versus antibiotic therapy.
In fact, the investigators enrolled 38 into each group to allow for attrition. Nevertheless, the study was stopped after an interim analysis. Of 16 patients in the infusion group, 13 (81%) had resolution of C. difficile–associated diarrhea after the first infusion. The 3 remaining patients received a second infusion with feces from a different donor, with resolution in 2 patients. Resolution of C. difficile infection occurred in only 4 of 13 patients (31%) receiving the antibiotic vancomycin.