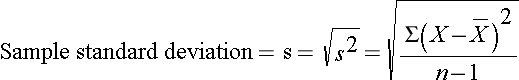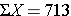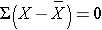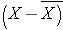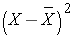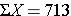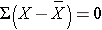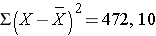Variance and Standard Deviation
If there are no extreme or outlying values of a variable, the mean is the most appropriate summary of a typical value, and to summarize variability in the data we specifically estimate the variability in the sample around the sample mean. If all of the observed values in a sample are close to the sample mean, the standard deviation will be small (i.e., close to zero), and if the observed values vary widely around the sample mean, the standard deviation will be large. If all of the values in the sample are identical, the sample standard deviation will be zero.
When discussing the sample mean, we found that the sample mean for diastolic blood pressure was 71.3. The table below shows each of the observed values along with its respective deviation from the sample mean.

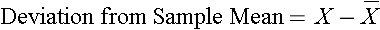
Table 11 - Diastolic Blood Pressures and Deviation from the Sample Mean
|
X=Diastolic Blood Pressure |
Deviation from the Mean |
|---|---|
|
76 |
4.7 |
|
64 |
-7.3 |
|
62 |
-9.3 |
|
81 |
9.7 |
|
70 |
-1.3 |
|
72 |
0.7 |
|
81 |
9.7 |
|
63 |
-8.3 |
|
67 |
-4.3 |
|
77 |
5.7 |
|
|
|
The deviations from the mean reflect how far each individual's diastolic blood pressure is from the mean diastolic blood pressure. The first participant's diastolic blood pressure is 4.7 units above the mean while the second participant's diastolic blood pressure is 7.3 units below the mean. What we need is a summary of these deviations from the mean, in particular a measure of how far, on average, each participant is from the mean diastolic blood pressure. If we compute the mean of the deviations by summing the deviations and dividing by the sample size we run into a problem. The sum of the deviations from the mean is zero. This will always be the case as it is a property of the sample mean, i.e., the sum of the deviations below the mean will always equal the sum of the deviations above the mean. However, the goal is to capture the magnitude of these deviations in a summary measure. To address this problem of the deviations summing to zero, we could take absolute values or square each deviation from the mean. Both methods would address the problem. The more popular method to summarize the deviations from the mean involves squaring the deviations (absolute values are difficult in mathematical proofs). Table 12 below displays each of the observed values, the respective deviations from the sample mean and the squared deviations from the mean.
Table 12
|
X=Diastolic Blood Pressure |
Deviation from the Mean
|
Squared Deviation from the Mean
|
|
76 |
4.7 |
22.09 |
|
64 |
-7.3 |
53.29 |
|
62 |
-9.3 |
86.49 |
|
81 |
9.7 |
94.09 |
|
70 |
-1.3 |
1.69 |
|
72 |
0.7 |
0.49 |
|
81 |
9.7 |
94.09 |
|
63 |
-8.3 |
68.89 |
|
67 |
-4.3 |
18.49 |
|
77 |
5.7 |
32.49 |
|
|
|
|
The squared deviations are interpreted as follows. The first participant's squared deviation is 22.09 meaning that his/her diastolic blood pressure is 22.09 units squared from the mean diastolic blood pressure, and the second participant's diastolic blood pressure is 53.29 units squared from the mean diastolic blood pressure. A quantity that is often used to measure variability in a sample is called the sample variance, and it is essentially the mean of the squared deviations. The sample variance is denoted s2 and is computed as follows:

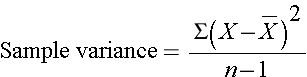
 |
Click below the question to view the answer. |
|
This content requires JavaScript enabled.
|
|
In this sample of n=10 diastolic blood pressures, the sample variance is s2 = 472.10/9 = 52.46. Thus, on average diastolic blood pressures are 52.46 units squared from the mean diastolic blood pressure. Because of the squaring, the variance is not particularly interpretable. The more common measure of variability in a sample is the sample standard deviation, defined as the square root of the sample variance: